La confesión de un crimen, las llamadas intrusivas y la teoría de juegos
La teoría de juegos te guía en situaciones complejas dónde hay que decidir qué estrategia tomar.
Un crimen por resolver
La cagamos. Lo teníamos todo calculado excepto lo concerniente al azar. Un grupo de personas, que durante el día son policías, salieron de la bolera dónde celebraban el ascenso de uno de ellos y Tyche nos puso en su camino. Tuvimos mala suerte.
Nos cazaron. Pero no tienen nada. Se escuchan sus voces nerviosas y cabreadas que provienen de la sala de al lado. Su mesa, acostumbrada a estar repleta de pruebas que incriminan a los detenidos, hoy resta vacía. A nosotros solo pueden condenarnos por un delito menor.
Nos tienen justo en frente. Saben lo que hemos hecho. Pero no hay forma de presentar una acusación mínimamente decente.
Me han separado de mi compañero. Llevo dos horas esperando en una fría sala de seis metros cuadrados, con una mesa de inoxidable en el centro y un par de sillas. Tras unos agitados pasos el inspector entra de un portazo y se dirige a mí con severidad:
-Hemos hablado con el juez y estamos dispuestos a ofrecerte un trato. Sabes que ahora solo podemos incriminaros por un delito menor que implicaría 1 año de cárcel a cada uno. Y que nos faltan pruebas para juzgaros por el caso completo. Así que vamos a pediros que confeséis. Si alguno decide hablar y colaborar para cerrar el caso, pueden ocurrir dos cosas: que uno decida confesar y el otro no, cosa que implicaría que el que ha confesado saldría libre y el otro estaría 20 años en la cárcel. O que los dos confesarais, iríais a la cárcel 5 años cada uno. En 2 horas volveré para que me digas qué vas a hacer.
Y vosotros, ¿qué haríais?
Esta narrativa presenta el enunciado del famosísimo dilema del prisionero. Es un ejemplo del tipo de problemas que estudia la teoría de juegos y que veremos que se puede asimilar a la situación de las llamadas promocionales de nuestras queridísimas compañías de internet.
John Nash, o Russell Crowe para los cinéfilos, demostró que para todas las situaciones que se pueden asimilar al dilema del prisionero existe una solución que representa un equilibrio en el que nadie querría cambiar de estrategia tomada y, por lo tanto, esa estrategia será la solución. A este escenario se le llama el equilibrio de Nash. Una solución en la que ninguno de sus participantes quiere cambiar de opción escogida mientras los demás mantengan las suyas.
Este equilibrio no garantiza el mayor bien común. No busca eso. Lo que encuentra es lo que buscamos todos de forma natural: no ser el pringado que se queda atrás.
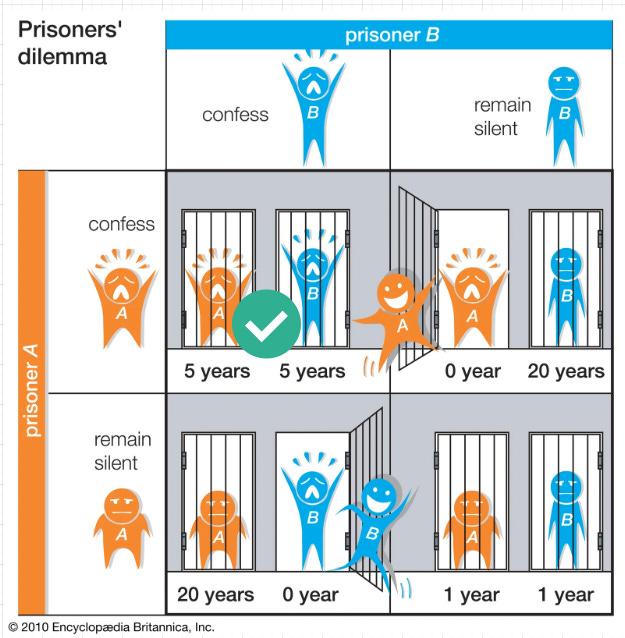
Si volvemos a la oferta del inspector al detenido veremos que el siguiente cuadro representa las distintas opciones:
El mejor escenario para el colectivo, para ambos criminales, es no confesar. Eso implicaría 2 años de prisión entre los dos, que es el mínimo al que pueden aspirar como pareja.
Pero Nash nos dice que eso da completamente igual. Seguramente si pudieran hablar entre ellos y acordar como abordar la situación pactarían callarse, pero están incomunicados y desconocen lo que hará el otro. En el caso de que el compañero decida no confesar, al protagonista de la historia le conviene confesar y salir libre. Por lo tanto, no confesar no es un equilibrio de Nash y no será la solución correcta.
El mejor escenario a nivel individual es confesar. Ya que si el compañero decide:
No confesar: Implica que el protagonista se libra de la cárcel. No tiene un escenario mejor.
Confesar: Ambos irán a la cárcel 5 años. En este escenario también ha escogido la mejor de las opciones, puesto que si el compañero va a confesar, es mejor que el protagonista también haya confesado y así evita los 20 años.
Por lo tanto, el equilibrio de Nash se encuentra en el escenario en que ambos confiesan y van a la cárcel por 5 años.
Muchos estaréis pensando que este ejercicio es una pantomima y que si existe una solución óptima a nivel genérico que además es la mejor solución individual la gente la escogerá. Diréis “son colegas, seguro que deciden no confesar y salen ambos al cabo de 1 año”.
Si fuese así… ¿Estaríamos tan preocupados por ir a la moda? ¿O Por lo que nuestros vecinos opinen de nosotros? ¿Las empresas contaminarían los ríos? ¿Los políticos dejarían de hacer ejercicios de propaganda constantes y se pondrían a resolver los problemas del pueblo a largo plazo? ¿Seguiríamos ignorando la insostenibilidad del sistema de pensiones español?
Todos estos ejemplos son situaciones que se pueden modelizar utilizando el mismo esquema que el dilema del prisionero. El político centrado en el bien común y no tanto en la propaganda cae fuera del equilibrio de Nash, con lo que queda eliminado de la partida. Pero tranquilos, un nuevo populista o demagogo ocupará su lugar.
Las grandes de internet
Si ahora recuperamos el ejemplo de la semana pasada sobre las campañas telefónicas de las empresas que te ofrecen servicios de internet, vemos que también se puede modelizar con el mismo modelo.
Como podemos ver en la imagen anterior, que representa las cuotas de mercado del sector de telefonía móvil e internet de 2021, estamos frente a un oligopolio dónde 4 empresas se reparten el 87% del mercado. Cualquier movimiento que haga uno de ellos va a afectar al sistema.
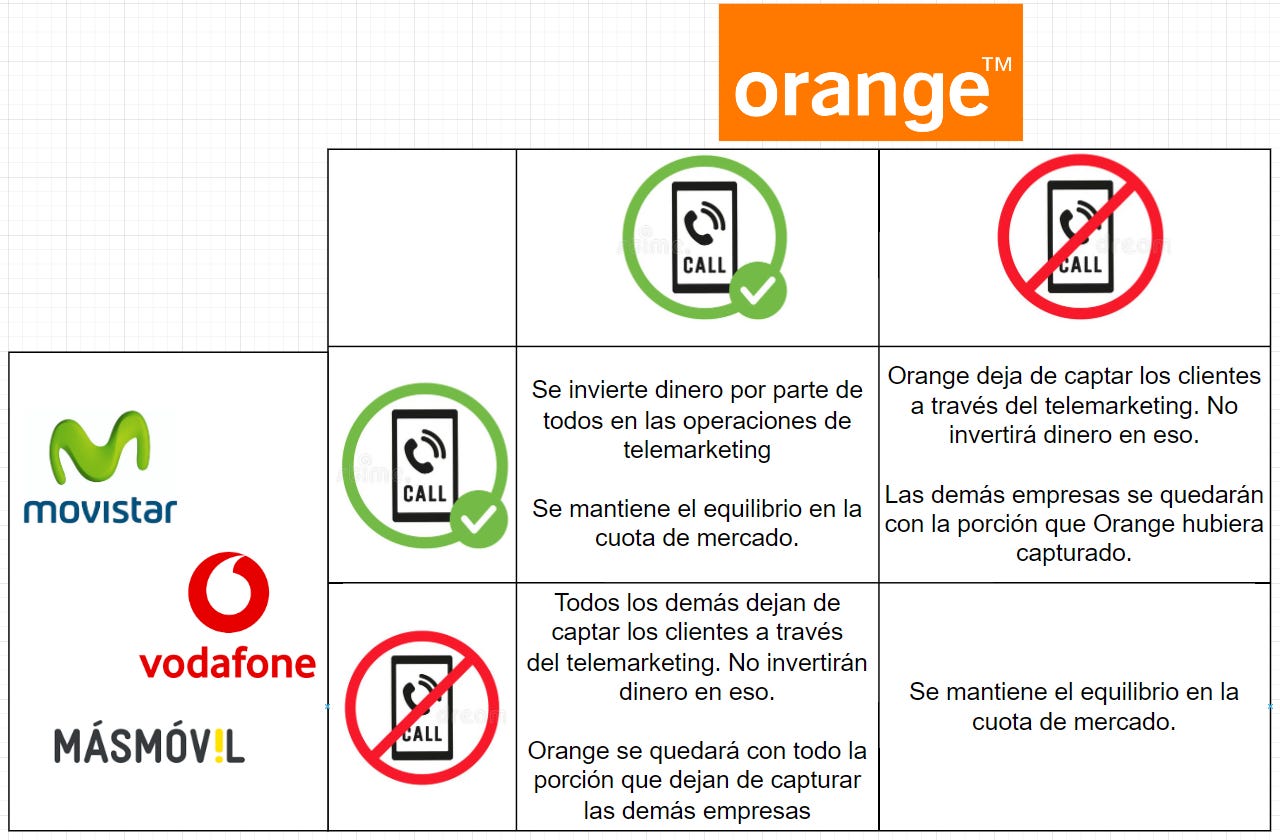
¿Qué pasaría si uno de los 4 grandes decidiera dejar de acosar telefónicamente la gente? Vamos a simplificar mucho el problema para poder centrarnos en lo que nos interesa. Supongamos que su forma de hacer márquetin (aparte del acoso telefónico) es el mismo para todos y que los productos y servicios ofrecidos son igual de buenos. Si quitamos todos estos factores vemos que podemos reducir el problema a lo que vemos en el siguiente gráfico:
Si Orange decidiera salirse de la norma de las llamadas de telemarketing veríamos que perdería una cantidad significativa de clientes que absorbería la competencia. Eso no se lo pueden permitir.
Está claro que el escenario ideal para todos, incluso para los consumidores, es el escenario en qué ninguno de ellos te llame a las 10 de la noche ni un sábado a la hora de la siesta. Pero esa solución no es un equilibrio de Nash, ya que si partiendo de ese escenario, solo uno de ellos decidiera romper con la situación y empezar a hacer llamadas, se quedaría con todo el pastel.
Me sabe mal, pero parece que no van a dejar de llamarnos.
La complejidad de obtener un buen modelo
Eduardo Sáenz contaba en una entrevista con Jordi Wild que explicó el dilema del prisionero en una cárcel. Los reclusos no estaban de acuerdo con la solución que Eduardo les presentaba. Ellos lo tenían claro: “yo no confieso”, le decían. El motivo que le exponían a Eduardo era el miedo a las represalias en caso si alguien confiesa.
Esto significa que el dilema del prisionero no lo teníamos bien modelizado. Estábamos suponiendo que el coste en cada uno de los casos eran únicamente los años de cárcel. Nada más lejos de la realidad. El modelo completo tiene que integrar a todos los factores que dependan del escenario e impliquen un coste/beneficio para cada individuo.
Al conjunto de normas que nos definen la relación entre costes y beneficios de un individuo en función del escenario, lo llamaremos función de coste.
Con la ayuda de la percepción de los reclusos, vemos que la función de coste del dilema del prisionero debería de incluir la parte de represalias, aparte de los años de cárcel. La mayor parte de posibles jugadores dará más valor a las represalias que a los años de cárcel en sí. Esto nos revela dónde se encuentra el verdadero equilibrio de Nash, que se ha desplazado hasta el escenario dónde ninguno va a confesar.
Recordemos que el equilibrio de Nash se encuentra en ese escenario dónde ninguno de los jugadores quiere cambiar su estrategia, ya que la alternativa sería peor a nivel individual. Ahora esto solo ocurre para el caso en el que uno decido no confesar, puesto que nunca querría cambiar de estrategia y arriesgarse a sufrir las represalias.
Un razonamiento muy parecido es el que Joan Tubau y José Luis Ferreira comentaban en el podcast de Kapital. Durante los últimos 70 años, el motivo por el cual los países querían tener armas nucleares no era por el hecho de utilizarlas contra el enemigo, más bien al contrario, presentarlas como elemento disuasorio para que el enemigo no los atacase a ellos con armas nucleares.
Los países que pudieron, decidieron disponer de armas nucleares para garantizar las represalias a cualquiera que se planteara atacarlos. Era más potente decir que tenían armas, que las armas en sí.
Definir la función de coste
Es importante tener bien definida la situación antes de decidir qué estrategia tomar. Hay que construir un buen modelo. Saber qué escenarios existen y qué costes hay que poner en cada escenario. Pero no siempre es tan fácil como en el ejercicio académico del dilema del prisionero. A continuación veremos un conjunto de factores que añaden complejidad a la construcción del modelo:
Medir el coste de algo intangible es sumamente complejo. Yo sé contar billetes o años de cárcel. Pero tengo más dificultad para contar cuanto “vale” para mí un año de cárcel. ¿Si os pagasen 100 euros, aceptaríais ir a la cárcel un año? ¿Y si en vez de 100€ son 10.000.000€? Y si ya resulta difícil saber eso para uno mismo, imaginaros intentar interpretar lo que vale para los demás.
Por otro lado, no todo el mundo comparte toda la información para que el juego se pueda operar correctamente. En muchas empresas podemos ver esto materializado si analizamos el salto entre lo que la gente dice que quiere y lo que realmente quiere a nivel personal. La falta de sinceridad añade una capa de oscuridad sobre el juego. No tener claro lo que la otra parte puede ganar o perder en función del escenario complica el análisis, pero no lo inutiliza.
Ligado a estas incertidumbres os diré dos cosas:
Para este tipo de problemas siempre existe una función de coste, aunque no sepamos calcularla.
Puede haber diferencias entre el valor real de la función de coste y el valor percibido por parte de uno de los jugadores. Hay que tener en cuenta que el jugador decidirá su estrategia en función de su perspectiva. El valor percibido es el valor importante en la negociación. (Ejemplo: En una estafa, el comprador cree que el valor que va a recibir es justo, este sería su valor percibido. El real, en este caso, estaría por debajo)
No dejéis nunca fuera las partes que no son obvias, puesto que muchas veces son las más relevantes. El juego seguirá siendo válido, pero os tocará esforzaros para definir correctamente los valores a situar en cada casilla.
Fernando Alonso, en su Podcast de píldoras del conocimiento, dedica un episodio entero a la teoría de juegos desde un punto de visto muy ameno. Sus reflexiones creo que pueden aportar mucha riqueza a este apartado en concreto.
Reflexiones personales y estrategias de negociación
Me hablaron de la teoría de juegos por primera vez en el 2006. Un buen amigo estaba haciendo un trabajo académico basado en la teoría de juegos y estuvimos hablando bastante sobre el tema durante un verano.
No tardé mucho en comprarme un par de libros sobre el tema e incluso hice algún curso MOOC. Desde entonces es un recurso que me permite romper las situaciones complejas que requieren tomar decisiones en un conjunto de cuadritos, funciones de coste y probabilidades. A aquellos que dispongáis de un poco de tiempo os recomiendo encarecidamente leer algunos libros sobre el tema. Veréis que el dilema del prisionero es una ínfima parte de todo lo que alberga la teoría de juegos.
Basarte en teoría de juegos para hacer frente a problemas complejos es una estrategia muy positiva. Puedes proponer soluciones que sepas que encajan como equilibrios de Nash. Eso te permite anticiparte a la elección del otro. La clave está en ayudar a construir el sistema de antemano para que el equilibrio se sitúe en el sitio que deseas.
Una estrategia complementaria es la de buscar juegos de suma positiva. Lo que en la jerga del business se llama el win-win. Por ejemplo, en la relación que tu empresa tenga con algunos proveedores os convendrá a ambos potenciar el camino del win-win. Relaciones dónde claramente todos salen ganando a la larga, a cambio de no sacar un pellizco extra a corto plazo.
Saber encarar las situaciones para que la otra parte vea las ventajas de tu propuesta es gran parte del éxito de la negociación. Luego, la teoría de juegos hará el resto.
A lo largo de las semanas tocaremos muchos temas en esta Newsletter, y ya os confieso que no dejaremos los juegos atrás fácilmente. Serán una herramienta a la que volveremos una y otra vez.
Eduard Bosch - STRATEGEMENT - Del contexto a la ejecución